
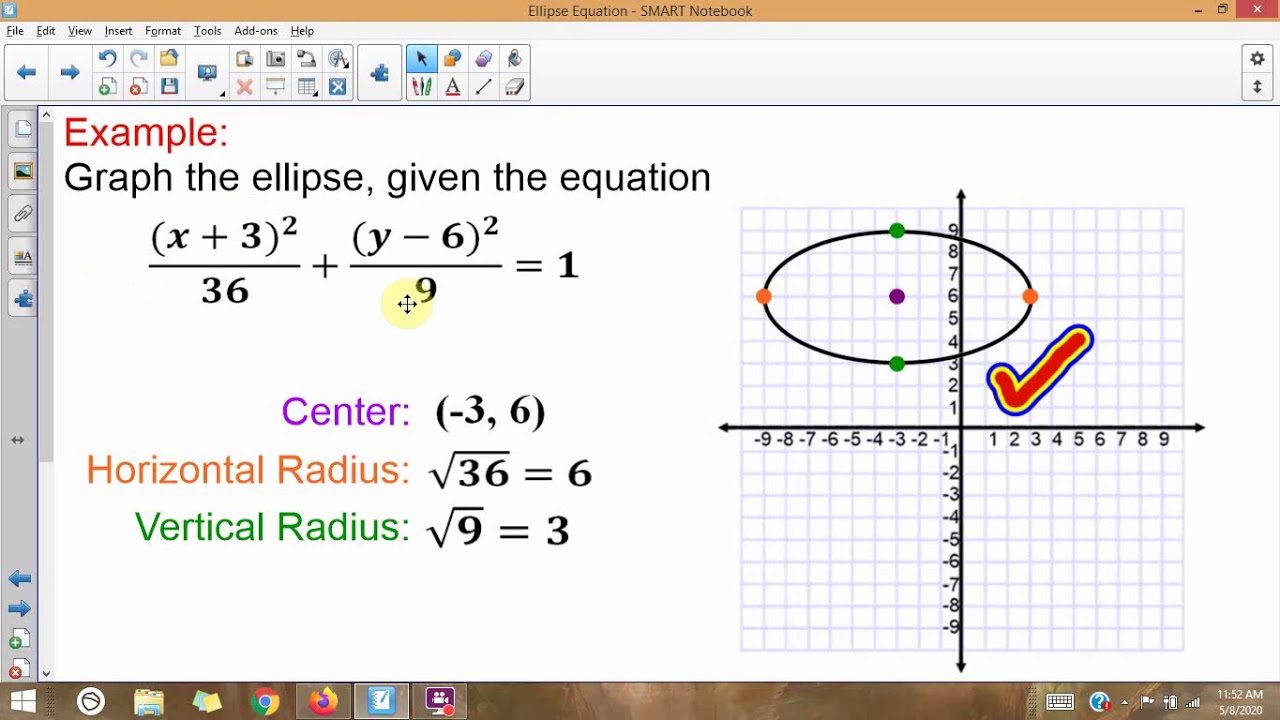
Put more simply, and without having to change definitions, when an ellipse is oriented horizontally, then the value of a is greater than b, and when it is oriented vertically, then the value of a is less than b. If it instead aligns with the vertical axis, then a is the distance from the center to the ellipse’s vertical vertex, and b is the distance from the center to the ellipse’s horizontal vertex. Note: the definitions of a and b above assume the semi-major axis aligns with the horizontal axis. When an ellipse is oriented horizontally, then the value of a is greater than b, and when it is oriented vertically, then the value of a is less than b.įor an ellipse that is centered at a point other than the origin (0, 0), the standard form equation for the ellipse is:
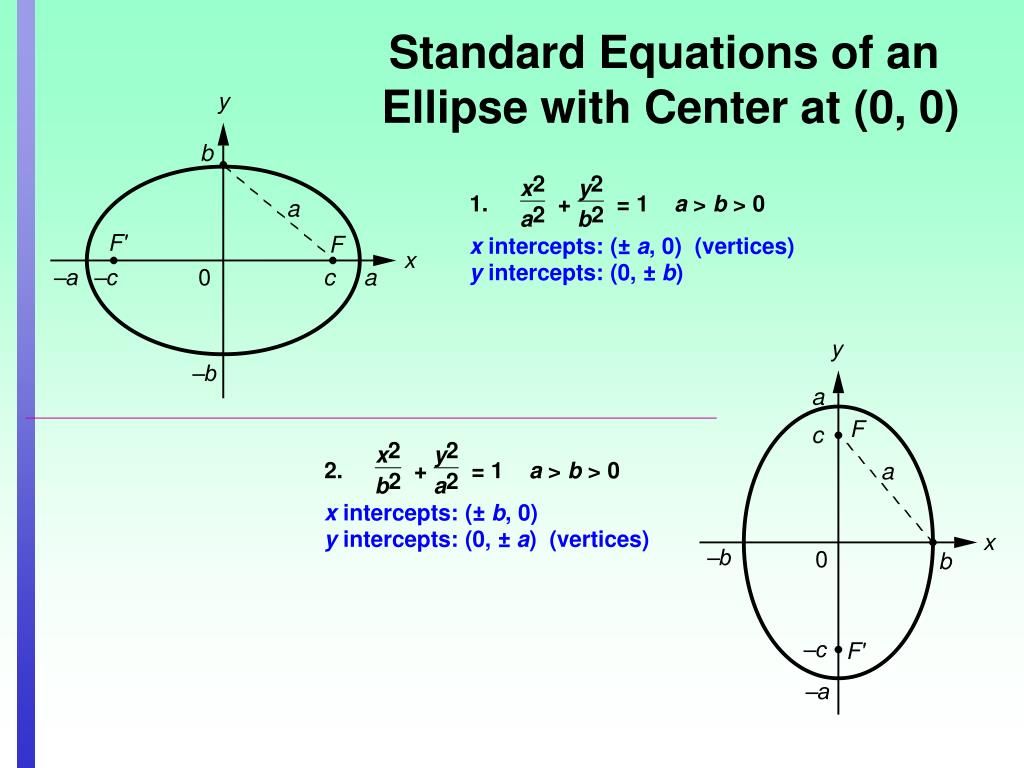
Using the semi-major axis a and semi-minor axis b, the standard form equation for an ellipse centered at origin (0, 0) is:Ī = distance from the center to the ellipse’s horizontal vertexī = distance from the center to the ellipse’s vertical vertex
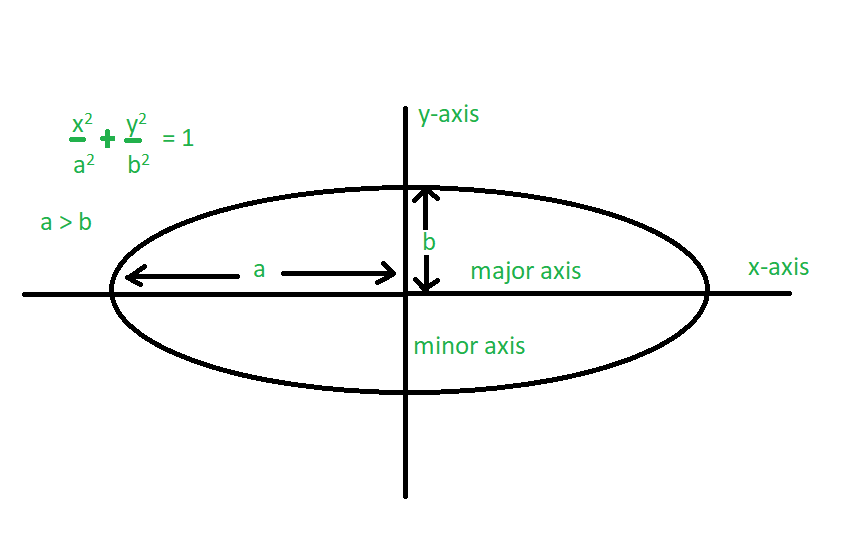
The semi-minor axis is defined as the lesser of the maximum horizontal and vertical extents of the ellipse’s curve. The semi-major axis is defined as the distance between the center of the ellipse and the maximum horizontal or vertical extent of its curve (also known as its horizontal or vertical vertex), whichever is greater. These maximum extents lie on the semi-major and semi-minor axes that bisect the ellipse horizontally and vertically. I think they have unconditional money back guarantee, so you do not have the chance of loosing anything.While an ellipse is oval in shape, it differs from an oval in that it is mathematically defined, while any curve resembling a squashed circle is an oval.Īn ellipse is described by the distance from its center to the maximum horizontal and vertical extent of the curve. is the site which I think will give you details. Just typing in the algebra problem and clicking on Solve, Algebrator generates step-by-step solution to the problem, and my math homework would be ready. I have used it frequently through several math classes – Intermediate algebra, College Algebra and Algebra 1. Syntehtic division, subtracting exponents and absolute values were a nightmare for me until I found Algebrator, which is truly the best math program that I have come across. Can I try it once?įrom: floating in the light, never forgotten Recommended by experts ! I must say this tool sounds really interesting. But could you let me know the details of authentic sites from where I can make the purchase? Can I get the Algebrator cd from a local book mart available in my area? Hello there, Thanks for the instantaneous response. I am a mathematics tutor who give private tuitions to pupils and I advocate Algebrator to my students since that aids them a lot when they sit to work out their homework by themselves at home. Hi, Algebrator offered at the site can be of great aid to you. Is there any guru who can lend me a helping hand?
Boy! This thing is really awful ! I just never seem to understand the point behind any topic. Hello all, I just began my ellipse graph calculator class. Holt california chapter 7 test answers mathematics | Quadratic equations square root property calculator |


 0 kommentar(er)
0 kommentar(er)
